
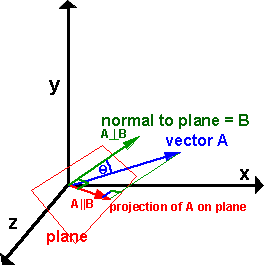
Thus the vector (1/3)A is a unit normal vector for this plane. Thus for a plane (or a line), a normal vector can be divided by its length to get a unit normal vector.Įxample: For the equation, x + 2y + 2z = 9, the vector A = (1, 2, 2) is a normal vector. Any nonzero vector can be divided by its length to form a unit vector. X = 11.Ī unit vector is a vector of length 1. But since P is on the plane, if we set X = P, we must get the correct value of d. Solution: The equation must be (1, 2, 3). Find the equation of the plane through P = (1, -1, 4) with normal vector A. What is a normal vector for this line?Įxample: Finding a plane when the normal is known. How is this line related to m and OA? Finally, find an equation for line OA. Check that lines OA and m are perpendicular. On graph paper plot the line m with equation 2x + 3y = 6 and also plot the point A = (2,3). This also means that vector OA is orthogonal to the plane, so the line OA is perpendicular to the plane.Ĭareful: It is NOT true that for any point P in the plane, A is orthogonal to P (unless d = 0).Įxercise: Show that if A is a normal vector to a plane, and k is a nonzero constant, then kA is also a normal vector to the same plane.ĭebate: For any plane, is the 0 vector orthogonal to all the direction vectors of the plane?Įxercise on Lines in the Plane: The same reasoning works for lines. Thus the coefficient vector A is a normal vector to the plane. This means that vector A is orthogonal to the plane, meaning A is orthogonal to every direction vector of the plane.Ī nonzero vector that is orthogonal to direction vectors of the plane is called a normal vector to the plane. This means that the vector A is orthogonal to any vector PQ between points P and Q of the plane.īut the vector PQ can be thought of as a tangent vector or direction vector of the plane.
If P and Q are in the plane with equation A. The equation of a line in the form ax + by + cz = d can be written as a dot product:

The equation of a line in the form ax + by = c can be written as a dot product: Dot Product and Normals to Lines and Planes Dot Product and Normals to Lines and Planes


 0 kommentar(er)
0 kommentar(er)
