

Prasolov, V.V., Tikhomirov, V.M.: Geometry. Peterson, M.A.: The geometry of Piero della Francesca. Ostermann, A., Wanner, G.: Geometry by Its History. Martini, H., Weissbach, B.: Napoleon’s theorem with weights in n-space. Liberti, L., Lavor, C., Maculan, N., Mucherino, A.: Euclidean distance geometry and applications. Lawes, C.P.: Proof without words: the length of a triangle median via the parallelogram law.
Krantz, S.G., McCarthy, J.E., Parks, H.R.: Geometric characterizations of centroids of simplices. Johnson, R.A.: Advanced Euclidean Geometry. Izumi, S.: Sufficiency of simplex inequalities. Hungerbühler, N.: Proofs without words: the area of the triangle of the medians has three-fourths the area of the original triangle. Honsberger, R.: Episodes in Nineteenth and Twentieth Century Euclidean Geometry. Hersh, R.: Heron’s formula: what about a tetrahedron? Coll. Heath, T.L.: The Thirteen Books of Euclid’s Elements, 2nd edn. Hajja, M., Walker, P.: The Gergonne and Nagel centers of a tetrahedron. Hajja, M., Martini, H., Spirova, M.: New extensions of Napoleon’s theorem to higher dimensions. Hajja, M.: The Gergonne and Nagel centers of an n-dimensional simplex. Gerber, L.: The orthocentric simplex as an extreme simplex. solution, ibid, 86, 387 (2013)įiedler, M.: Isodynamic systems in Euclidean spaces and an n-dimensional analogue of a theorem by Pompeiu. 76, 193–203 (2003)Įdmonds, A.L., Hajja, M., Martini, H.: Coincidences of simplex centers and related facial structures. 68, 914–917 (1961)Ĭrabb, R.A.: Gaspard Monge and the Monge point of the tetrahedron. Springer, Berlin (1994)īlumenthal, L.M.: A budget of curiosa metrica. XYZ Press, LLC (2016)īalk, M.B., Boltyanskij, V.G.: Geometry of Masses.
(1964)Īndreescu, T., Korsky, S., Pohoata, C.: Lemmas in Olympiad Geometry. 125, 612–622 (2018)Īl-Afifi, G., Hajja, M., Hamdan, A., Krasopoulos, P.T.: Pompeiu-like theorems for the medians of a simplex. Springer, Berlin (2004)Īl-Afifi, G., Hajja, M., Hamdan, A.: Another n-dimensional generalization of Pompeiu’s theorem. The mean is the average of all numbers: Add all the values and divide the sum by the number of values.Abrosimov, N.V., Makai Jr., E., Mednykh, A.D., Nikonorov, Y.G., Rote, G.: The infimum of the volumes of convex polytopes of any given facet areas is 0. The mode refers to the most repetitive number in the given dataset. The range is the difference between the highest and the lowest values. The mode is the most frequently occurring value in a set of given numbers. The median is the middle score in a set of given numbers. The mean is the arithmetic average of a given dataset. Original set: th term] What is the Difference Between Mean, Median, Mode, and Range? Step 1: Arrange the data items in ascending order. Median = /2Įxample: The age of the members of a weekend poker team has been listed below. The median formula of a given set of numbers say having 'n' even number of observations, can be expressed as: The median formula of a given set of numbers, say having 'n' odd number of observations, can be expressed as: Step 3: Check if the number of observations 'n' is even or odd.Step 2: Secondly, count the total number of observations 'n'.Step 1: Arrange the data in ascending or descending order.The following steps are helpful while applying the median formula for ungrouped data. The following set of formulas would help in finding the median of the given data. The median formula varies based on the number of observations and whether they are odd or even. For finding this measure of central tendency, it is necessary to write the components of the group in increasing order.
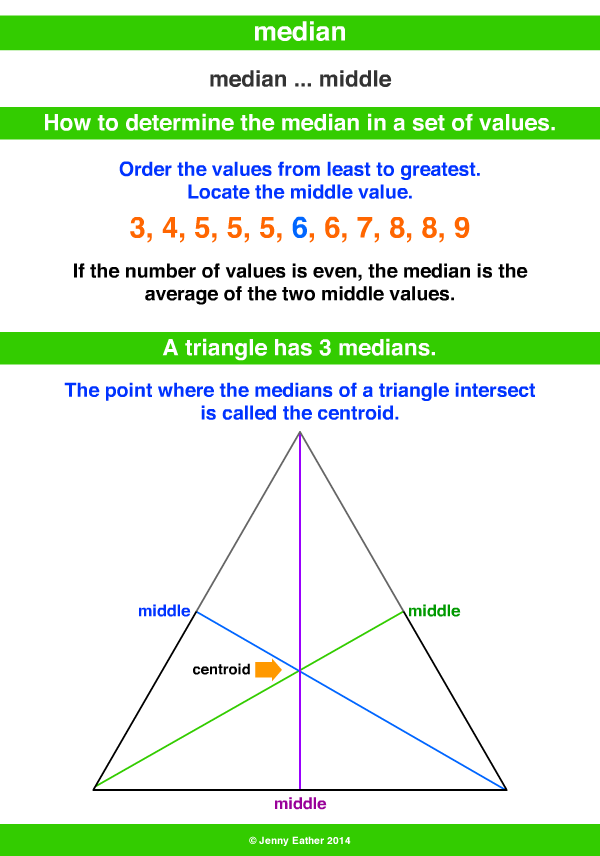
Using the median formula, the middle value of the arranged set of numbers can be calculated. Let's arrange this data in ascending order: 2, 3, 4, 4, 6.


 0 kommentar(er)
0 kommentar(er)
